Problemas de ecuaciones de segundo grado (Rise Above Hate) :

Problema 1

La suma de dos números es 10 y la suma de sus cuadrados es 58. Halle ambos números

Primero se asigna la variable x a una de las incógnitas del problema. Hay dos incógnitas que son ambos números, como el problema no hace distinción entre uno y otro, puede asignarse x a cualquiera de los dos, por ejemplo:

x = Primer número

Como la suma de ambos es 10, entonces necesariamente el otro será:

10 − x = Segundo número

Para entenderlo mejor:

Si entre su amigo y usted tienen $ 1.000, y su amigo tiene $ 400, ¿Cuánto tiene usted?, obviamente, restando el total menos 400, es decir 1.000 − 400 = $ 600. Si su amigo tiene $ x, la cuenta no cambia, sólo que no sabrá el valor sino en función de x, es decir, usted tiene 1.000 − x .

La condición final del problema establece que la suma de los cuadrados de ambos números resulta 58, entonces:

x² + (10 - x)² = 58

Esta es la ecuación a resolver

Para hacerlo, aplicamos algunas técnicas de álgebra elemental y luego reordenamos para llegar a la fórmula conocida.

Vemos que la operación indicada entre paréntesis es el cuadrado de un binomio. Es un error muy común que los estudiantes escriban: (a − b)² = a² − b²,  lo cual es incorrecto. La expresión correcta es: (a − b)² = a² − 2•a•b + b²

Desarrollando la ecuación se tiene: x² + 10² − 2•10•x + x² = 58 = x² + 100 − 20•x + x² = 58

Ordenando y agrupando: 2x² − 20•x+ 42 = 0;

Dividiendo entre 2 toda la ecuación:

 x² − 10x + 21 = 0

Ahora podemos aplicar la fórmula general para resolver la ecuación de segundo grado y llegaremos a x₁ = 7 y x₂ = 3.

Veamos, si tenemos

a = 1,                b = −10        c = 21

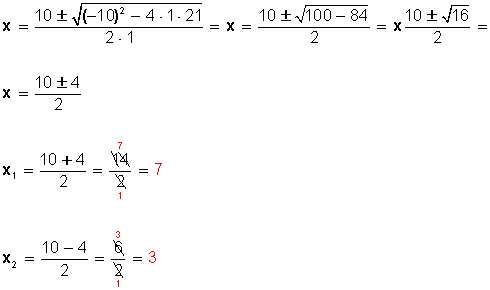
Los números buscados son 7 y 3.

Problema 2

El largo de una sala rectangular es 3 metros mayor que el ancho. Si el ancho aumenta 3 m y el largo aumenta 2 m, el área se duplica. Halle el área original de la sala.

Largo y ancho son diferentes. El problema permite que la variable x se asigne a cualquiera de las dos incógnitas, largo o ancho.

Supongamos que:

x = ancho de la sala

El largo es 3 metros mayor que el ancho, así es que:

x + 3 = largo de la sala.

El área de un rectángulo es la multiplicación de ambos:

x • (x + 3 ) = área de la sala.

Téngase en cuenta que estos son los datos iniciales.

Las condiciones del problema explican que el ancho aumenta en 3 metros y el largo aumenta en 2 metros, así que, luego del aumento quedan:

x + 3 = nuevo ancho de la sala

x + 5 = nuevo largo de la sala

(x + 3 ) • (x + 5) = nueva área de la sala

Según los datos del problema, el área se ha duplicado, así es que planteamos la ecuación:

(x + 3 ) • (x + 5) = 2 • x • (x + 3)

Se efectúan las multiplicaciones: x² + 5x + 3x + 15 = 2x² + 6x

Se pasa todo al primer miembro: x² + 5x + 3x + 15 − 2x² − 6x = 0

Se simplifica: − x2 + 2x + 15 = 0 Esta es la ecuación a resolver.

Se aplica la fórmula conocida y resulta: x₁ = 5 y x₂ = −3.

La solución x = −3 se desecha, ya que x es el ancho de la sala y no puede ser negativo. Se toma como única respuesta que el ancho original (x) era 5 metros.

Como el largo inicial  x + 3 = 8 metros, el área original era 8m • 5m = 40 m².

Problema 3

Halle el área y perímetro del triángulorectángulo mostrado. Las dimensiones están en metros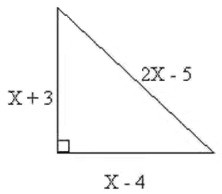 

Como es un triángulo rectángulo se cumple el Teorema de Pitágoras: "El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos" (c² = a² + b²). La hipotenusa es el lado mayor (2x − 5) y los otros dos son los catetos, se plantea entonces la ecuación:

(x + 3)² + (x − 4)² = (2x − 5)²

Desarrollando cada binomio al cuadrado, se tiene:

x² + 2 • 3 • x + 3² + x² − 2 • 4 • x + 4² = (2x)² − 2 • (2x) • 5 + 5² = x² + 6x + 9 + x² − 8x + 16 = 4x² − 20x + 25

Reagrupando:

x² + 6x + 9 + x² − 8x + 16 − 4x² + 20x − 25 = 0

Finalmente:

−2x² + 18x = 0

Es la ecuación a resolver

Las raíces de la ecuación son x₁ = 0 y x₂ = 9.

La solución x = 0 se desecha, ya que entonces un cateto sería −4 m, lo cual no es posible. La solución es entonces, x = 9. De esta manera, el triángulo queda con catetos 12 metros y 5 metros y con hipotenusa 13 metros.

El área de un triángulo es base por altura dividido 2; la base y la altura son los dos catetos que están a 90° , por lo tanto el área es

El perímetro es la suma de los lados, es decir, P = 12 m + 5 m + 13 m = 30 m.

Problema 4:
Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.
Edad actual  x
Edad hace 13 años  x − 13
Edad dentro de 11 años  x + 11



Edad actual  21


Problema 5:
Un jardín rectangular de 50 m de largo por 34 m de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es 540 m².

(50 + 2x) · (34 + 2x) − 50 · 34 = 540
4x² + 168x − 540 = 0        x² + 42x − 135 = 0
x = 3 y x = −45

La anchura del camino es 3 m .